Calcul de la Perméabilité Équivalente d'un Sol Stratifié
Contexte : L'écoulement de l'eau dans les sols.
La perméabilitéCapacité d'un sol à laisser l'eau s'écouler à travers ses vides. Elle est quantifiée par le coefficient de perméabilité k, généralement en m/s. est une propriété fondamentale en mécanique des sols qui régit la vitesse à laquelle l'eau s'écoule à travers un sol sous l'effet d'un gradient hydraulique. Dans la nature, les sols sont rarement homogènes. On rencontre très souvent un massif de sol hétérogèneUn volume de sol composé de plusieurs couches ou zones ayant des propriétés différentes (granulométrie, perméabilité, compressibilité, etc.)., constitué de couches de natures différentes superposées horizontalement. Cet exercice vise à déterminer une perméabilité "équivalente" pour un tel massif, c'est-à-dire la perméabilité d'un sol homogène fictif qui se comporterait de la même manière que le sol stratifié réel.
Remarque Pédagogique : Cet exercice vous apprendra à modéliser l'écoulement de l'eau dans un milieu complexe et à comprendre pourquoi un sol stratifié ne se comporte pas de la même manière selon que l'eau le traverse horizontalement ou verticalement. C'est un concept clé pour les études de drainage, de stabilité des pentes ou de transport de polluants.
Objectifs Pédagogiques
- Comprendre l'anisotropie de la perméabilité dans un sol stratifié.
- Savoir calculer la perméabilité équivalente pour un écoulement parallèle aux couches (\(k_{\text{éq,h}}\)).
- Savoir calculer la perméabilité équivalente pour un écoulement perpendiculaire aux couches (\(k_{\text{éq,v}}\)).
- Interpréter le rapport d'anisotropie et ses conséquences pratiques.
Données de l'étude
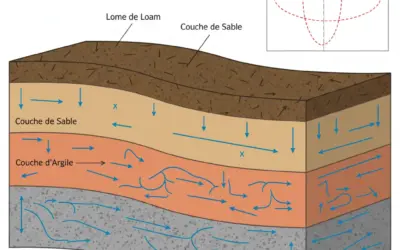
Schéma du Massif de Sol Stratifié
| Couche | Nature du sol | Épaisseur (\(H_i\)) [$\text{m}$] | Perméabilité (\(k_i\)) [$\text{m/s}$] |
|---|---|---|---|
| 1 | Sable fin | 2.0 | \(5 \times 10^{-5}\) |
| 2 | Argile silteuse | 1.5 | \(2 \times 10^{-8}\) |
| 3 | Sable graveleux | 3.0 | \(1 \times 10^{-3}\) |
Questions à traiter
- Calculer la perméabilité équivalente horizontale (\(k_{\text{éq,h}}\)) du massif de sol.
- Calculer la perméabilité équivalente verticale (\(k_{\text{éq,v}}\)) du massif de sol.
- Calculer le rapport d'anisotropie (\(k_{\text{éq,h}} / k_{\text{éq,v}}\)) et interpréter le résultat.
Les bases en Mécanique des Sols
Pour résoudre cet exercice, il est essentiel de comprendre la loi de Darcy et les principes de base de l'écoulement en milieu stratifié.
1. Loi de Darcy
La loi de Darcy stipule que le débit d'eau (\(Q\)) à travers une section de sol (\(A\)) est proportionnel au coefficient de perméabilité (\(k\)) et au gradient hydraulique (\(i\)).
\[ Q = k \cdot i \cdot A \]
2. Écoulement parallèle aux couches (Horizontal)
Lorsque l'écoulement est parallèle aux couches, le gradient hydraulique est le même pour toutes les couches. Le débit total est la somme des débits dans chaque couche. La perméabilité équivalente est une moyenne pondérée par les épaisseurs.
3. Écoulement perpendiculaire aux couches (Vertical)
Lorsque l'écoulement est perpendiculaire aux couches, la vitesse de filtration (\(v = Q/A\)) est la même à travers toutes les couches. La perte de charge totale est la somme des pertes de charge dans chaque couche. La perméabilité équivalente est une moyenne harmonique.
Correction : Calcul de la Perméabilité Équivalente
Question 1 : Calculer la perméabilité équivalente horizontale (\(k_{\text{éq,h}}\))
Principe (le concept physique)
Pour un écoulement horizontal, on imagine que les couches de sol sont comme des autoroutes superposées. L'eau a la "même envie" de traverser chaque autoroute (le gradient hydraulique 'i' est constant). Le débit total est simplement la somme des débits qui passent dans chaque autoroute. On cherche la perméabilité d'une autoroute unique et fictive qui aurait le même débit total.
Mini-Cours (approfondissement théorique)
Ce cas est analogue à un circuit électrique avec des résistances en parallèle. La "facilité de passage" (conductance, équivalente à \(k \cdot H\)) de chaque couche s'additionne. La perméabilité équivalente \(k_{\text{éq,h}}\) est donc une moyenne des perméabilités individuelles \(k_i\), pondérée par les épaisseurs respectives \(H_i\).
Remarque Pédagogique (le conseil du professeur)
Pensez "chemin de moindre résistance". L'eau s'écoulera préférentiellement dans la couche la plus perméable. Attendez-vous donc à ce que le résultat de \(k_{\text{éq,h}}\) soit fortement influencé par, et proche de, la plus grande valeur de perméabilité des couches du massif.
Normes (la référence réglementaire)
Ce principe de calcul n'est pas directement une "norme" mais une loi fondamentale de l'hydraulique des sols. Il constitue la base des calculs de débits et de rabattement de nappe que l'on retrouve dans les recommandations géotechniques et les normes de conception comme l'Eurocode 7.
Formule(s) (l'outil mathématique)
Hypothèses (le cadre du calcul)
- L'écoulement est laminaire et permanent (loi de Darcy valide).
- Le sol est saturé en eau et incompressible.
- Les couches de sol sont homogènes, isotropes et d'étendues horizontales infinies.
Donnée(s) (les chiffres d'entrée)
| Paramètre | Couche 1 | Couche 2 | Couche 3 |
|---|---|---|---|
| Épaisseur \(H_i\) [$\text{m}$] | 2.0 | 1.5 | 3.0 |
| Perméabilité \(k_i\) [$\text{m/s}$] | \(5 \times 10^{-5}\) | \(2 \times 10^{-8}\) | \(1 \times 10^{-3}\) |
Astuces (Pour aller plus vite)
Lors du calcul de la somme \(\sum (k_i \cdot H_i)\), repérez le terme dominant. Ici, \(k_3 \cdot H_3\) (\(3 \times 10^{-3}\)) est beaucoup plus grand que les autres. Le résultat final sera de l'ordre de \(k_3 \cdot H_3 / H_T\), ce qui permet de vérifier rapidement l'ordre de grandeur de votre calcul.
Schéma (Avant les calculs)
Calcul(s) (l'application numérique)
Calcul de l'épaisseur totale \(H_T\)
Calcul de la somme pondérée \(\sum (k_i \cdot H_i)\)
Calcul de \(k_{\text{éq,h}}\)
Schéma (Après les calculs)
Réflexions (l'interprétation du résultat)
La valeur de \(k_{\text{éq,h}}\) (\(4.77 \times 10^{-4} \text{ m/s}\)) est très proche de la perméabilité de la couche la plus perméable (Couche 3, \(1 \times 10^{-3} \text{ m/s}\)) mais est "diluée" par les autres couches. Cela confirme que pour un écoulement horizontal, le débit est gouverné par la couche la plus drainante. La couche d'argile, bien que quasi-imperméable, n'a presque aucun impact sur le débit horizontal car l'eau la contourne en passant par les couches plus perméables.
Points de vigilance (les erreurs à éviter)
L'erreur la plus fréquente est de faire une simple moyenne arithmétique des perméabilités. Il est crucial de pondérer chaque perméabilité par l'épaisseur de sa couche. Assurez-vous également de la cohérence de toutes vos unités avant de commencer le calcul.
Points à retenir (permettre a l'apprenant de maitriser la question)
- Écoulement horizontal \(\Rightarrow\) Gradient hydraulique constant.
- Écoulement horizontal \(\Rightarrow\) Les débits s'additionnent.
- Écoulement horizontal \(\Rightarrow\) La formule est une moyenne pondérée par les épaisseurs.
- Écoulement horizontal \(\Rightarrow\) Le résultat est tiré vers la plus forte perméabilité.
Le saviez-vous ? (la culture de l'ingénieur)
Les couches de sable et de gravier très perméables sont appelées des "aquifères". Ce sont ces formations géologiques que l'on cible pour le pompage d'eau potable. Une couche d'argile intercalée peut créer un "aquifère captif", où l'eau est sous pression, pouvant donner lieu à des puits artésiens jaillissants.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant)
Si l'épaisseur de la couche de sable graveleux (Couche 3) n'était que de 1.0 m, quelle serait la nouvelle valeur de \(k_{\text{éq,h}}\) (en \(10^{-4} \text{ m/s}\)) ? (Nouvelle épaisseur totale = 4.5 m)
Question 2 : Calculer la perméabilité équivalente verticale (\(k_{\text{éq,v}}\))
Principe (le concept physique)
Pour un écoulement vertical, on imagine l'eau traversant les couches en série, l'une après l'autre. Le débit qui traverse la première couche doit obligatoirement traverser la deuxième, puis la troisième. La vitesse de l'eau (le débit par unité de surface) est donc la même partout. En revanche, l'effort nécessaire pour traverser chaque couche (la perte de charge) s'additionne.
Mini-Cours (approfondissement théorique)
Ce cas est analogue à un circuit électrique avec des résistances en série. La "résistance" hydraulique de chaque couche (\(H_i / k_i\)) s'additionne pour donner la résistance totale du massif. La perméabilité équivalente \(k_{\text{éq,v}}\) est donc une moyenne harmonique des perméabilités individuelles, pondérée par les épaisseurs.
Remarque Pédagogique (le conseil du professeur)
Pensez "goulot d'étranglement". Le débit total sera limité par la couche la plus difficile à traverser, c'est-à-dire la moins perméable. Attendez-vous à ce que le résultat de \(k_{\text{éq,v}}\) soit très proche de, et même inférieur à, la plus faible valeur de perméabilité des couches du massif.
Normes (la référence réglementaire)
Comme pour l'écoulement horizontal, ce principe est une loi fondamentale de l'hydraulique des sols. Il est crucial pour les calculs de temps de consolidation des argiles (tassement des fondations) ou pour la conception de barrières d'étanchéité (géomembranes, couches d'argile compactée).
Formule(s) (l'outil mathématique)
La formule découle de l'égalité des pertes de charge : \(\Delta h_{\text{total}} = \sum \Delta h_i\). En utilisant la loi de Darcy (\(v = k \cdot i = k \cdot \Delta h / H\)) et en simplifiant, on obtient :
Hypothèses (le cadre du calcul)
- L'écoulement est laminaire et permanent (loi de Darcy valide).
- Le sol est saturé en eau et incompressible.
- Les couches de sol sont homogènes, isotropes et d'étendues horizontales infinies.
Donnée(s) (les chiffres d'entrée)
| Paramètre | Couche 1 | Couche 2 | Couche 3 |
|---|---|---|---|
| Épaisseur \(H_i\) [$\text{m}$] | 2.0 | 1.5 | 3.0 |
| Perméabilité \(k_i\) [$\text{m/s}$] | \(5 \times 10^{-5}\) | \(2 \times 10^{-8}\) | \(1 \times 10^{-3}\) |
Astuces (Pour aller plus vite)
Lors du calcul du dénominateur \(\sum (H_i / k_i)\), repérez le terme le plus grand. C'est celui où \(k_i\) est le plus petit. Ici, \(H_2/k_2\) sera gigantesque par rapport aux autres. Le résultat final de \(k_{\text{éq,v}}\) sera donc proche de \(H_T / (H_2/k_2)\), ce qui permet de vérifier l'ordre de grandeur.
Schéma (Avant les calculs)
Calcul(s) (l'application numérique)
Calcul de la somme \(\sum (H_i / k_i)\)
Calcul de \(k_{\text{éq,v}}\)
Schéma (Après les calculs)
Réflexions (l'interprétation du résultat)
La valeur de \(k_{\text{éq,v}}\) (\(8.66 \times 10^{-8} \text{ m/s}\)) est extrêmement proche de celle de la couche la moins perméable (Couche 2, \(2 \times 10^{-8} \text{ m/s}\)). Cela confirme que l'écoulement vertical est dicté par le maillon le plus faible. La présence d'une fine couche d'argile peut rendre un massif, même composé majoritairement de sables très perméables, quasi-imperméable dans la direction verticale.
Points de vigilance (les erreurs à éviter)
Attention à la domination par la faible perméabilité ! Le terme \(\frac{1.5}{2 \times 10^{-8}}\) est de l'ordre de \(10^7\), tandis que les autres termes sont de l'ordre de \(10^3-10^4\). Une petite erreur sur la perméabilité de cette couche aura un impact énorme sur le résultat final. Faites attention aux puissances de 10 lors du calcul.
Points à retenir (permettre a l'apprenant de maitriser la question)
- Écoulement vertical \(\Rightarrow\) Vitesse de filtration constante.
- Écoulement vertical \(\Rightarrow\) Les pertes de charges s'additionnent.
- Écoulement vertical \(\Rightarrow\) La formule est une moyenne harmonique.
- Écoulement vertical \(\Rightarrow\) Le résultat est tiré vers la plus faible perméabilité.
Le saviez-vous ? (la culture de l'ingénieur)
Cette propriété est mise à profit pour la construction des centres de stockage de déchets. On y construit des "barrières passives" en compactant des couches d'argile de très faible perméabilité sous les déchets, pour empêcher les polluants (lixiviats) de s'infiltrer verticalement et de contaminer les nappes phréatiques.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant)
Si la perméabilité de la couche d'argile (Couche 2) était de \(k_2 = 1 \times 10^{-7} \text{ m/s}\), quelle serait la nouvelle valeur de \(k_{\text{éq,v}}\) (en \(10^{-7} \text{ m/s}\)) ?
Question 3 : Calculer le rapport d'anisotropie et interpréter
Principe (le concept physique)
Le rapport d'anisotropie est une mesure de la "préférence directionnelle" de l'écoulement. Il compare la facilité de l'écoulement dans la direction horizontale par rapport à la direction verticale. Un rapport supérieur à 1 indique que le sol est plus perméable horizontalement que verticalement, ce qui est presque toujours le cas pour les sols sédimentaires.
Mini-Cours (approfondissement théorique)
L'anisotropie est une propriété tensorielle. Dans un modèle 2D, le tenseur de perméabilité a deux composantes principales, \(k_h\) et \(k_v\). Ce rapport est crucial en modélisation numérique des écoulements souterrains. Une forte anisotropie déforme les "lignes de courant" et les "lignes équipotentielles", qui ne sont plus perpendiculaires entre elles.
Remarque Pédagogique (le conseil du professeur)
Ne soyez pas surpris par des valeurs très élevées. Dans les formations géologiques réelles, des rapports de 100, 1000, voire plus, sont courants. Cela traduit simplement la présence de couches continues très peu perméables qui bloquent l'écoulement vertical mais n'affectent pas l'écoulement horizontal.
Normes (la référence réglementaire)
La prise en compte de l'anisotropie est une exigence dans les modélisations géotechniques avancées pour les grands projets (barrages, tunnels, excavations profondes). Ne pas en tenir compte peut conduire à une sous-estimation drastique des débits de pompage ou à une mauvaise prédiction de la propagation des polluants.
Formule(s) (l'outil mathématique)
Hypothèses (le cadre du calcul)
Ce calcul suppose que les perméabilités équivalentes \(k_{\text{éq,h}}\) et \(k_{\text{éq,v}}\) ont été déterminées correctement et représentent bien les directions principales de l'écoulement.
Donnée(s) (les chiffres d'entrée)
On utilise les résultats des deux questions précédentes.
- \(k_{\text{éq,h}} \approx 4.77 \times 10^{-4} \text{ m/s}\)
- \(k_{\text{éq,v}} \approx 8.66 \times 10^{-8} \text{ m/s}\)
Astuces (Pour aller plus vite)
Pour estimer rapidement l'ordre de grandeur, divisez la perméabilité la plus élevée du massif par la plus faible. Ici, \(10^{-3} / 10^{-8} = 10^5\). Le rapport d'anisotropie réel sera plus faible mais du même ordre de grandeur.
Schéma (Avant les calculs)
Calcul(s) (l'application numérique)
Calcul du rapport d'anisotropie
Schéma (Après les calculs)
Réflexions (l'interprétation du résultat)
Un rapport de plus de 5500 est extrêmement élevé. Cela signifie que l'eau s'écoulera plus de 5500 fois plus facilement et rapidement à travers ce massif en suivant les couches (horizontalement) qu'en les traversant (verticalement). Cette forte anisotropie est une caractéristique typique des dépôts sédimentaires où des couches perméables (sables) alternent avec des couches quasi-imperméables (argiles).
Points de vigilance (les erreurs à éviter)
Attention à ne pas inverser le rapport (\(k_v / k_h\)). Le rapport d'anisotropie est conventionnellement défini comme le rapport de la perméabilité maximale sur la minimale, qui est presque toujours \(k_h / k_v\) dans les sols stratifiés.
Points à retenir (permettre a l'apprenant de maitriser la question)
Le rapport d'anisotropie \(k_{\text{éq,h}} / k_{\text{éq,v}}\) quantifie à quel point l'écoulement est plus facile horizontalement que verticalement. Une valeur > 1 indique un sol anisotrope. Une valeur très > 1 indique une forte anisotropie, typique d'une alternance de couches très perméables et très peu perméables.
Le saviez-vous ? (la culture de l'ingénieur)
Cette anisotropie a des conséquences majeures en génie civil. Par exemple, lors du pompage dans une nappe phréatique au sein d'un tel massif, le rabattement de la nappe (le cône de dépression) sera beaucoup plus étendu horizontalement que profondément. C'est également un facteur déterminant dans la vitesse de migration horizontale d'un polluant.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant)
Si \(k_{\text{éq,h}} = 2 \times 10^{-4} \text{ m/s}\) et \(k_{\text{éq,v}} = 5 \times 10^{-6} \text{ m/s}\), quel est le rapport d'anisotropie ?
Outil Interactif : Influence d'une couche peu perméable
Utilisez les curseurs pour modifier l'épaisseur et la perméabilité de la couche d'argile (Couche 2) et observez en temps réel son impact sur les perméabilités équivalentes globales du massif.
Paramètres de la Couche 2 (Argile)
Résultats Clés
Quiz Final : Testez vos connaissances
1. Dans un sol stratifié, l'écoulement horizontal est principalement contrôlé par :
2. L'écoulement vertical à travers un sol stratifié est principalement contrôlé par :
3. Si toutes les couches d'un massif avaient la même perméabilité, le rapport d'anisotropie \(k_{\text{éq,h}}/k_{\text{éq,v}}\) serait :
4. Quelle est l'hypothèse principale de la loi de Darcy ?
5. Une forte anisotropie de perméabilité (\(k_h \gg k_v\)) signifie que :
Glossaire
- Perméabilité (k)
- Aptitude d'un sol à se laisser traverser par l'eau. Le coefficient de perméabilité k, exprimé en m/s, quantifie cette propriété. Plus k est élevé, plus le sol est perméable.
- Gradient Hydraulique (i)
- Rapport de la perte de charge (différence de hauteur d'eau) sur la distance d'écoulement. C'est le "moteur" de l'écoulement. Il est sans dimension.
- Anisotropie
- Caractéristique d'un matériau dont les propriétés (ici, la perméabilité) dépendent de la direction considérée. Un sol stratifié est typiquement anisotrope.
D’autres exercices de mécanique des sols:













0 commentaires