Calcul du Facteur de Dommage (D) de Hoek-Brown
Contexte : La mécanique des roches et le critère de Hoek-BrownUn critère de rupture empirique utilisé pour estimer la résistance des massifs rocheux fracturés..
Lors de l'excavation d'ouvrages souterrains (tunnels, galeries, mines), le massif rocheux encaissant est inévitablement perturbé par le processus de creusement. Cette perturbation, qui se traduit par une fracturation et une décompression de la roche, réduit sa résistance mécanique près de la paroi de l'excavation. Le Facteur de Dommage (D)Un facteur empirique, variant de 0 (aucun dommage) à 1 (dommage très important), qui quantifie la réduction de résistance du massif rocheux due à la méthode d'excavation. du modèle de Hoek-Brown est un paramètre essentiel qui permet de quantifier cet effet. Cet exercice vous guidera dans la sélection d'une valeur de D appropriée en fonction de la méthode d'excavation.
Remarque Pédagogique : Cet exercice illustre comment des observations qualitatives de terrain (la qualité d'une excavation) sont traduites en un paramètre quantitatif pour les calculs de stabilité, un processus fondamental en ingénierie géotechnique.
Objectifs Pédagogiques
- Comprendre le rôle et l'importance du facteur de dommage (D) dans le critère de Hoek-Brown.
- Apprendre à sélectionner une valeur de D appropriée en se basant sur la description d'une méthode d'excavation.
- Identifier l'impact du facteur D sur les autres paramètres du modèle de Hoek-Brown.
Données de l'étude
Fiche Technique du Massif Rocheux
| Caractéristique | Valeur |
|---|---|
| Type de roche | Granite |
| Résistance à la compression uniaxiale de la roche intacte, \( \sigma_{\text{ci}} \) | 85 MPa |
| Constante du matériau intact, \( m_{\text{i}} \) | 17 |
| Indice de Résistance Géologique, GSIGeological Strength Index. Un indice visuel qui caractérise la qualité structurale d'un massif rocheux, de très bonne (GSI élevé) à très mauvaise (GSI faible). | 65 (massif de bonne qualité, fracturé en blocs) |
Schéma de l'Excavation du Tunnel
Questions à traiter
- La méthode d'excavation retenue est un "sautage contrôlé de bonne qualité". En vous basant sur les recommandations de Hoek, Carranza-Torres et Corkum (2002), déterminez la valeur la plus appropriée pour le facteur de dommage (D).
- En utilisant la valeur de D déterminée à la question 1 et le GSI de 65, calculez les paramètres du massif rocheux \( m_{\text{b}} \) et \( s \).
- Si, en raison de contraintes de chantier, la méthode d'excavation était un "sautage conventionnel de qualité moyenne" (D = 0.8), quelles seraient les nouvelles valeurs de \( m_{\text{b}} \) et \( s \)? Comparez-les aux résultats de la question 2 et commentez l'impact sur la résistance du massif.
- Écrivez l'équation complète du critère de rupture de Hoek-Brown pour les conditions initiales (sautage de bonne qualité), en utilisant les paramètres que vous avez calculés.
Les bases sur le Critère de Hoek-Brown
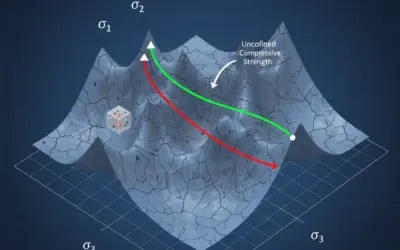
Le critère de Hoek-Brown est une relation empirique qui permet de définir l'enveloppe de rupture d'un massif rocheux. Il relie la contrainte principale majeure (\( \sigma'_{\text{1}} \)) à la contrainte principale mineure (\( \sigma'_{\text{3}} \)) au moment de la rupture.
1. Formule Générale du Critère de Hoek-Brown (2002)
La formule s'écrit :
\[ \sigma'_{\text{1}} = \sigma'_{\text{3}} + \sigma_{\text{ci}} \left( m_{\text{b}} \frac{\sigma'_{\text{3}}}{\sigma_{\text{ci}}} + s \right)^a \]
Où :
- \( \sigma_{\text{ci}} \) est la résistance en compression uniaxiale de la roche intacte.
- \( m_{\text{b}}, s, a \) sont des constantes dépendant de la qualité du massif rocheux.
2. Le Facteur de Dommage (D)
Les paramètres \( m_{\text{b}} \) et \( s \) sont calculés à partir du GSI et du facteur de dommage D :
\[ m_{\text{b}} = m_{\text{i}} \exp\left(\frac{\text{GSI} - 100}{28 - 14D}\right) \]
\[ s = \exp\left(\frac{\text{GSI} - 100}{9 - 3D}\right) \]
Le facteur D est un nombre entre 0 et 1 qui représente l'ampleur de la perturbation du massif rocheux due aux méthodes d'excavation. Une valeur de 0 signifie aucun dommage (par exemple, une excavation mécanique très soignée), tandis qu'une valeur de 1 représente des dommages très importants (sautage lourd en espace confiné).
Correction : Calcul du Facteur de Dommage (D) de Hoek-Brown
Question 1 : Déterminer le facteur de dommage (D)
Principe (le concept physique)
Le principe ici est de traduire une observation physique — la qualité d'une excavation et la perturbation visible de la roche environnante — en un paramètre numérique utilisable dans un modèle de calcul. On quantifie le "dommage" pour pouvoir en tenir compte dans l'évaluation de la résistance du massif rocheux.
Mini-Cours (approfondissement théorique)
Autour de toute excavation souterraine, il se crée une "zone endommagée" (ou "Excavation Damage Zone" - EDZ). Dans cette zone, le processus de creusement (par exemple, les vibrations du sautage) a créé de nouvelles micro-fractures et a ouvert les fractures pré-existantes. La roche y est donc plus déformable et moins résistante que le massif "vierge" situé plus loin. Le facteur D est une manière simple de modéliser l'effet de cette EDZ.
Remarque Pédagogique (le conseil du professeur)
En ingénierie géotechnique, il est fondamental de lier les observations de terrain aux modèles de calcul. Avant de vous précipiter sur une formule, demandez-vous toujours : "Quelle est l'observation physique que je cherche à modéliser ?". Ici, c'est la qualité du creusement.
Normes (la référence réglementaire)
La méthode et les valeurs de référence pour le facteur D sont principalement basées sur les recommandations publiées par Evert Hoek et ses collaborateurs, notamment dans l'article de 2002 : "Hoek, E., Carranza-Torres, C., and Corkum, B. (2002). Hoek-Brown failure criterion – 2002 edition.". Ces recommandations sont devenues une pratique standard dans le domaine.
Formule(s) (l'outil mathématique)
Pour cette première question, il n'y a pas de formule à appliquer. La détermination de D est une démarche empirique basée sur une sélection dans une table de correspondance.
Hypothèses (le cadre du calcul)
- On suppose que la description "sautage contrôlé de bonne qualité" est une représentation fidèle de la réalité du chantier.
- On admet que la table de Hoek, développée à partir de nombreux cas réels, est applicable au contexte de notre projet (type de roche, échelle de l'ouvrage).
Donnée(s) (les chiffres d'entrée)
| Paramètre | Description |
|---|---|
| Méthode d'excavation | "Sautage contrôlé de bonne qualité" |
Astuces (Pour aller plus vite)
Dans les rapports géotechniques, cette valeur de D est souvent l'un des premiers paramètres fixés. Mémorisez les 3 valeurs clés : D=0 pour une excavation mécanique parfaite (TBM), D=0.5-0.8 pour du sautage, et D=1.0 pour un cas très dégradé. Cela vous donnera un ordre de grandeur immédiat.
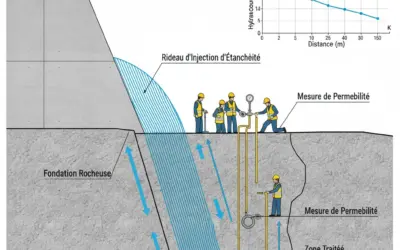
Schéma (Avant les calculs)
Ce schéma illustre conceptuellement comment différentes méthodes d'excavation affectent l'étendue de la zone endommagée (et donc le facteur D).
Impact de la méthode d'excavation sur la zone endommagée
Calcul(s) (l'application numérique)
La résolution est une simple lecture de la table de référence. On cherche la ligne correspondant à notre description.
| Description de la perturbation du massif | Valeur suggérée de D |
|---|---|
| Excavation mécanique (Tunnelier, raise boring) d'excellente qualité. | 0.0 |
| Très bon sautage contrôlé ou excavation mécanique de bonne qualité. | 0.5 |
| Sautage conventionnel ou mécanique de qualité moyenne. | 0.8 |
| Sautage de très mauvaise qualité. | 1.0 |
Schéma (Après les calculs)
Le schéma suivant résume le processus de sélection menant au résultat final.
Processus de sélection du facteur D
Réflexions (l'interprétation du résultat)
La valeur D=0.5 représente un compromis réaliste. On reconnaît que le sautage, même bien contrôlé, endommage la roche, mais on considère que les techniques utilisées (plans de tirs, explosifs adaptés) ont permis de limiter cette perturbation à un niveau modéré. Ce chiffre unique va maintenant "réduire" la résistance du massif dans toutes les étapes suivantes du calcul.
Points de vigilance (les erreurs à éviter)
Ne confondez pas la qualité de la roche (décrite par le GSI) et la qualité de l'excavation (décrite par D). On peut avoir un excellent massif rocheux (GSI élevé) mais le dégrader fortement par un mauvais sautage (D élevé), et inversement.
Points à retenir (permettre a l'apprenant de maitriser la question)
Pour maîtriser cette étape, retenez que :
- Le facteur D est un lien direct entre une pratique de chantier (la méthode de creusement) et un paramètre de calcul.
- Sa valeur est empirique et se choisit dans des tables de référence basées sur l'expérience.
- Une valeur faible de D correspond à une faible perturbation et donc à une meilleure qualité d'excavation.
Le saviez-vous ? (la culture de l'ingénieur)
Les techniques de "sautage contrôlé" (ou "smooth blasting") ont été développées dans les années 50 et 60, notamment en Suède. L'idée est de créer une ligne de fracture nette en périphérie de l'excavation en utilisant des charges explosives faibles et très rapprochées, tirées en dernier. Cela évite que les ondes de choc des tirs principaux ne se propagent et ne fracturent le massif rocheux final.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Quelle serait la valeur de D si l'excavation était réalisée avec un tunnelier (TBM), produisant des parois lisses et sans fracturation visible ?
Question 2 : Calcul des paramètres \( m_{\text{b}} \) et s
Principe (le concept physique)
Le principe est de traduire la qualité globale du massif (GSI) et le dommage dû à l'excavation (D) en deux paramètres qui décrivent le comportement mécanique du massif : \(m_{\text{b}}\), qui représente la friction entre les blocs de roche, et \(s\), qui représente la cohésion ou la "tenue" globale du massif.
Mini-Cours (approfondissement théorique)
Dans le critère de Mohr-Coulomb, la résistance est décrite par une cohésion (c) et un angle de friction (φ). Le critère de Hoek-Brown ne définit pas directement ces valeurs. Les paramètres \(m_{\text{b}}\) et \(s\) sont des constantes empiriques qui permettent de décrire une enveloppe de rupture non-linéaire (une courbe), plus réaliste pour les roches que la droite de Mohr-Coulomb. Un massif très fracturé et de mauvaise qualité aura des valeurs de \(m_{\text{b}}\) et \(s\) très faibles.
Remarque Pédagogique (le conseil du professeur)
Considérez ces formules comme la "recette de cuisine" du modèle. Vous prenez les ingrédients de base (GSI, \(m_{\text{i}}\), D) et vous les combinez pour obtenir les paramètres qui donneront sa "saveur" (sa résistance) au massif rocheux. La rigueur dans l'application de la recette est essentielle.
Normes (la référence réglementaire)
Les formules utilisées sont celles de l'édition 2002 du critère de Hoek-Brown (Hoek, Carranza-Torres, & Corkum).
Formule(s) (l'outil mathématique)
Formule pour le paramètre \( m_{\text{b}} \)
Formule pour le paramètre \( s \)
Hypothèses (le cadre du calcul)
- Les formules exponentielles sont considérées comme valides pour la plage de GSI de notre projet.
- Les valeurs de D déterminées à la question 1 sont correctes.
Donnée(s) (les chiffres d'entrée)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Indice de Résistance Géologique | GSI | 65 | - |
| Constante du matériau intact | \(m_{\text{i}}\) | 17 | - |
| Facteur de dommage | D | 0.5 | - |
Astuces (Pour aller plus vite)
Le terme \( (\text{GSI} - 100) \) sera toujours négatif. Par conséquent, les termes dans les exponentielles seront toujours négatifs, ce qui signifie que \(m_{\text{b}}\) sera toujours inférieur à \(m_{\text{i}}\) et \(s\) sera toujours inférieur à 1. Si vous obtenez un résultat différent, vérifiez vos signes !
Schéma (Avant les calculs)
Ce schéma conceptuel montre comment les données d'entrée (GSI, D, mi) sont utilisées dans les formules pour produire les paramètres de sortie (mb, s).
Flux de calcul des paramètres de Hoek-Brown
Calcul(s) (l'application numérique)
Nous procédons au calcul, étape par étape, pour chaque paramètre.
Calcul du paramètre \(m_{\text{b}}\)
Calcul du paramètre \(s\)
Schéma (Après les calculs)
Ce diagramme compare la valeur de la constante de la roche intacte (mi) avec la valeur réduite pour le massif rocheux (mb), illustrant la perte de résistance.
Réduction de la constante m de la roche intacte au massif
Réflexions (l'interprétation du résultat)
La valeur de \(m_{\text{b}}\) (3.210) est bien plus faible que celle de la roche intacte \(m_{\text{i}}\) (17). Cela reflète la perte de résistance due à la présence de fractures dans le massif (effet du GSI) et à leur perturbation par l'excavation (effet de D). La valeur de \(s\) est très faible (proche de zéro), ce qui indique que le massif rocheux fracturé a une très faible "cohésion" ; sa résistance dépend presque entièrement de la friction entre les blocs.
Points de vigilance (les erreurs à éviter)
La principale source d'erreur est le calcul des dénominateurs dans les exponentielles. Assurez-vous d'effectuer la multiplication par D avant la soustraction (priorité des opérations). Une erreur ici change radicalement le résultat.
Points à retenir (permettre a l'apprenant de maitriser la question)
Pour cette question, retenez que :
- \(m_{\text{b}}\) et \(s\) sont les paramètres finaux qui décrivent la résistance du massif rocheux endommagé.
- Ils dépendent de trois facteurs : la nature de la roche intacte (\(m_{\text{i}}\)), la qualité structurale du massif (GSI), et la méthode d'excavation (D).
- Un GSI ou un D plus faible mènent à des valeurs de \(m_{\text{b}}\) et \(s\) plus élevées (massif plus résistant).
Le saviez-vous ? (la culture de l'ingénieur)
Le paramètre \(s\) a une signification physique particulière : pour un massif rocheux totalement désagrégé (GSI=0), \(s\) devient nul. Cela signifie que le massif se comporte comme un tas de granulats sans cohésion, comme du sable. La résistance du massif ne dépend alors plus que de la friction entre les grains.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Si le massif était de moins bonne qualité (GSI=50) mais l'excavation parfaite (D=0), quelle serait la nouvelle valeur de \(m_{\text{b}}\) ?
Question 3 : Impact d'un sautage de qualité moyenne
Principe (le concept physique)
Cette question a pour but de quantifier la "perte de résistance" due à une méthode de construction moins soignée. En comparant les résultats de deux scénarios (bonne vs moyenne qualité), on peut évaluer concrètement l'importance de bien maîtriser les techniques d'excavation sur un chantier.
Mini-Cours (approfondissement théorique)
C'est une "analyse de sensibilité". En ingénierie, on fait très souvent varier un paramètre d'entrée (ici, D) pour voir son influence sur les résultats. Cela permet d'identifier les paramètres les plus influents et de comprendre les risques. Si une petite variation d'un paramètre entraîne une grande variation du résultat, ce paramètre est dit "sensible" et il faudra le déterminer avec une grande précision.
Remarque Pédagogique (le conseil du professeur)
Un bon ingénieur ne se contente pas de faire un seul calcul. Il en fait plusieurs pour explorer différents scénarios ("what if..."). Cette question vous entraîne à adopter cette démarche : que se passe-t-il si les conditions sur le chantier sont moins bonnes que prévu ?
Normes (la référence réglementaire)
La valeur de D=0.8 pour un "sautage conventionnel de qualité moyenne" provient de la même table de Hoek et al. (2002) que celle utilisée à la question 1.
Formule(s) (l'outil mathématique)
Formule pour le paramètre \( m_{\text{b}} \)
Formule pour le paramètre \( s \)
Hypothèses (le cadre du calcul)
L'hypothèse est qu'un changement de méthode d'excavation n'affecte que le paramètre D. Les autres paramètres (GSI, \(m_{\text{i}}\)) restent inchangés.
Donnée(s) (les chiffres d'entrée)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Indice de Résistance Géologique | GSI | 65 | - |
| Constante du matériau intact | \(m_{\text{i}}\) | 17 | - |
| Facteur de dommage (nouveau) | D | 0.8 | - |
Astuces (Pour aller plus vite)
Puisque D augmente, les dénominateurs (28-14D) et (9-3D) diminuent. Comme le numérateur (GSI-100) est négatif, le rapport devient plus négatif. L'exponentielle d'un nombre plus négatif donne un résultat plus petit. Vous devez donc vous attendre à trouver des valeurs de \(m_{\text{b}}\) et \(s\) plus faibles qu'à la question 2.
Schéma (Avant les calculs)
Le schéma suivant met en évidence le changement du paramètre d'entrée pour cette analyse de sensibilité.
Changement du paramètre d'entrée D
Calcul(s) (l'application numérique)
Calcul du nouveau paramètre \(m_{\text{b}}\)
Calcul du nouveau paramètre \(s\)
Schéma (Après les calculs)
Un diagramme en barres est idéal pour comparer les deux scénarios et visualiser la perte de résistance.
Comparaison de l'impact du facteur D
Réflexions (l'interprétation du résultat)
Commentaire : Le passage à un sautage de moins bonne qualité (D augmentant de 0.5 à 0.8) a un impact très significatif sur les paramètres de résistance. \(m_{\text{b}}\), qui est lié à la friction du massif, et \(s\), qui représente sa cohésion, diminuent tous les deux de manière drastique (respectivement -34% et -47%). Concrètement, cela signifie que le modèle considère le massif rocheux autour du tunnel comme étant beaucoup moins résistant. Cette dégradation de la résistance obligerait probablement les ingénieurs à prévoir un soutènement plus robuste (boulons plus rapprochés, béton projeté plus épais), ce qui augmenterait les coûts et la durée du projet.
Points de vigilance (les erreurs à éviter)
Lors d'une analyse de sensibilité, veillez à ne changer qu'un seul paramètre à la fois. Si vous aviez changé à la fois D et GSI, vous n'auriez pas pu isoler l'impact de la seule qualité de l'excavation.
Points à retenir (permettre a l'apprenant de maitriser la question)
Le message clé est que la qualité de l'exécution sur le chantier a une influence quantitative directe et majeure sur la sécurité et l'économie d'un projet. Un bon contrôle qualité pendant la construction est non seulement une bonne pratique, mais il permet de valider les hypothèses de calcul et d'éviter des surcoûts liés à des soutènements imprévus.
Le saviez-vous ? (la culture de l'ingénieur)
Dans les grands projets de tunnels, on réalise souvent une "galerie pilote" ou une "galerie de reconnaissance" de plus petit diamètre avant de creuser l'ouvrage principal. Cela permet, entre autres, de tester différentes méthodes de sautage, de mesurer in-situ l'étendue de la zone endommagée et de calibrer plus finement la valeur de D pour le reste du projet.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
Avec les paramètres de la question 3 (D=0.8), si le GSI était très bon (GSI=80), quelle serait la valeur de \(m_{\text{b}}\)?
Question 4 : Équation complète du critère de rupture
Principe (le concept physique)
L'objectif est de synthétiser tous les résultats précédents en une seule équation fonctionnelle. Cette équation représente le "modèle de comportement" final du massif rocheux. C'est cette relation mathématique qui sera utilisée par les ingénieurs pour prédire si la roche va rompre sous l'effet des contraintes.
Mini-Cours (approfondissement théorique)
L'équation \(\sigma'_{\text{1}} = f(\sigma'_{\text{3}})\) est appelée "enveloppe de rupture". Dans un diagramme où l'axe des abscisses est \(\sigma'_{\text{3}}\) et l'axe des ordonnées est \(\sigma'_{\text{1}}\), cette équation trace une courbe. Tout état de contrainte (\(\sigma'_{\text{3}}\), \(\sigma'_{\text{1}}\)) qui se trouve en dessous de la courbe est stable. Si un état de contrainte atteint la courbe, la rupture se produit.
Remarque Pédagogique (le conseil du professeur)
C'est l'aboutissement de votre travail. Vous êtes parti d'observations qualitatives et de données de base, et vous avez abouti à un outil de prédiction quantitatif. C'est l'essence même du métier d'ingénieur : créer des modèles pour anticiper le comportement de systèmes physiques complexes.
Normes (la référence réglementaire)
L'équation est l'expression finale du critère de Hoek-Brown, édition 2002.
Formule(s) (l'outil mathématique)
Formule pour l'exposant \(a\)
Formule générale du critère de rupture
Hypothèses (le cadre du calcul)
On suppose que le comportement du massif rocheux est bien représenté par le critère de Hoek-Brown, ce qui est généralement admis pour les massifs rocheux fracturés mais peut être moins précis pour des roches massives ou très déformables.
Donnée(s) (les chiffres d'entrée)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Indice de Résistance Géologique | GSI | 65 | - |
| Facteur de dommage | D | 0.5 | - |
| Résistance Roche Intacte | \(\sigma_{\text{ci}}\) | 85 | MPa |
| Paramètre du massif | \(m_{\text{b}}\) | 3.210 | - |
| Paramètre du massif | \(s\) | 0.00941 | - |
Astuces (Pour aller plus vite)
Pour des GSI supérieurs à 25, le paramètre \(a\) est toujours très proche de 0.5. Si vous faites un calcul rapide à la main, utiliser \(a=0.5\) est une approximation acceptable qui simplifie grandement les calculs (on obtient une racine carrée).
Schéma (Avant les calculs)
Ce schéma illustre le concept de l'enveloppe de rupture dans le plan des contraintes principales.
Concept de l'Enveloppe de Rupture
Calcul(s) (l'application numérique)
Il reste à calculer le dernier paramètre, \(a\), avant d'écrire l'équation finale.
Calcul de l'exposant \(a\)
Assemblage de l'équation finale
On substitue \( \sigma_{\text{ci}} = 85 \), \( m_{\text{b}} = 3.210 \), \( s = 0.00941 \) et \( a = 0.502 \) dans l'équation générale.
Schéma (Après les calculs)
Le résultat final est une équation qui peut être tracée. Le graphique ci-dessous montre l'enveloppe de rupture correspondante.
Enveloppe de Rupture de Hoek-Brown
Réflexions (l'interprétation du résultat)
Cette équation (et sa représentation graphique) est l'outil de prédiction final. Par exemple, si les calculs montrent que dans une zone de la paroi du tunnel, la roche est confinée par une contrainte \(\sigma'_{\text{3}}\) de 5 MPa, on peut utiliser l'équation pour calculer la résistance \(\sigma'_{\text{1}}\). Si la contrainte \(\sigma'_{\text{1}}\) réelle induite par le creusement dépasse cette résistance, la roche se rompra, et il faudra prévoir un soutènement.
Points de vigilance (les erreurs à éviter)
Assurez-vous que toutes vos contraintes sont en MPa pour être cohérent avec la valeur de \(\sigma_{\text{ci}}\). L'erreur la plus fréquente à ce stade est de mélanger les unités (par exemple, utiliser des kPa pour \(\sigma'_{\text{3}}\) avec une \(\sigma_{\text{ci}}\) en MPa).
Points à retenir (permettre a l'apprenant de maitriser la question)
La maîtrise de ce sujet implique de comprendre que l'équation finale de Hoek-Brown est une synthèse de toutes les caractéristiques du massif :
- La nature de la roche (\(\sigma_{\text{ci}}\), \(m_{\text{i}}\))
- Sa structure à grande échelle (GSI)
- La perturbation due aux travaux (D)
Le saviez-vous ? (la culture de l'ingénieur)
Le critère de Hoek-Brown a été développé initialement par Evert Hoek dans les années 1980 pour des projets de mines en roche dure. Il a été continuellement mis à jour depuis (la version 2002 utilisée ici est une des plus connues) pour intégrer de plus en plus de données et étendre son champ d'application à des roches de plus mauvaise qualité et à des projets de génie civil comme les tunnels.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
\( \sigma'_{\text{1}} = \sigma'_{\text{3}} + 85 \left( 3.210 \frac{\sigma'_{\text{3}}}{85} + 0.00941 \right)^{0.502} \)
A vous de jouer (pour verifier la comprehension de l'etudiant parrapport a la question)
En utilisant l'équation finale, quelle est la résistance à la compression uniaxiale (\(\sigma'_{\text{ci,massif}}\)) du massif rocheux ? (Astuce : la compression uniaxiale correspond à \(\sigma'_{\text{3}} = 0\)).
Outil Interactif : Influence de GSI et D sur les paramètres de Hoek-Brown
Utilisez les curseurs pour voir comment l'indice de qualité du massif (GSI) and le facteur de dommage (D) influencent les paramètres de calcul du modèle de Hoek-Brown. La constante \(m_{\text{i}}\) est fixée à 17 pour le granite.
Paramètres d'Entrée
Paramètres de Hoek-Brown Calculés
Quiz Final : Testez vos connaissances
1. Une valeur de D = 1.0 représente :
2. Lequel de ces paramètres de Hoek-Brown est indépendant du facteur de dommage D ?
3. Une excavation avec un Tunnelier (TBM) est généralement associée à quelle valeur de D ?
4. Si l'indice GSI d'un massif rocheux augmente, cela signifie que :
5. La constante du matériau intact (\(m_{\text{i}}\)) dépend principalement :
Glossaire
- Critère de Hoek-Brown
- Un critère de rupture empirique (basé sur l'expérience) utilisé internationalement pour estimer la résistance mécanique des massifs rocheux fracturés.
- Facteur de Dommage (D)
- Un paramètre empirique, variant de 0 (aucun dommage) à 1 (dommage très important), qui quantifie la réduction de résistance du massif rocheux due à la fracturation et à la décompression induites par la méthode d'excavation.
- GSI (Geological Strength Index)
- L'Indice de Résistance Géologique est un système de classification permettant d'estimer la qualité d'un massif rocheux en se basant sur sa structure (de intacte/massive à très fracturée/broyée) et l'état des surfaces des discontinuités (de très rugueuses et saines à lisses et altérées).
D'autres exercices de mécanique des roches:














0 commentaires